Può essere utile, a questo punto, riportare alcune nozioni di fotometria, anche al fine di far risaltare come la definizione metrologica delle grandezze luminose operi una radicale restrizione della ricchezza presente nel lessico corrente, introducendo in compenso una elevato grado di precisione terminologica, tipico dei linguaggi specialistici.

Non si vuole con questo contrapporre il lessico “quantitativo” della scienza a quello “qualitativo” del linguaggio comune, ma soltanto sottolineare la necessità di un loro sviluppo contestuale e l’opportunità di un reciproco arricchimento.

L’INTENSITA’ LUMINOSA delle sorgenti I

L’intensità luminosa I è la grandezza fotometrica fondamentale.

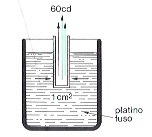La sua unità di misura, la candela ( cd ), è definita come la sessantesima parte dell’intensità luminosa emessa dal corpo nero di Burgess alla temperatura di fusione del platino, perpendicolarmente ad una superficie di 1 cm quadrato di area. ( Nelle semplici esperienze che ci proponiamo di realizzare in questo percorso, potremo assumere che una comune candela stearica abbia una intensità non molto lontana da quella fotometrica ).

L’angolo piano α e l’angolo solido Ω

Per definire le altre grandezze fotometriche è necessario richiamare brevemente le definizioni di angolo piano e di angolo solido.  

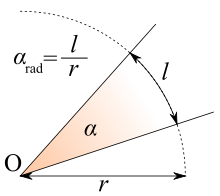
Occorre far presente che nel Sistema Internazionale ( SI ) l’unità di misura per gli angoli non è il grado sessagesimale, al quale siamo abituati, ma il radiante ( rad ), definito come l’angolo al centro che in una circonferenza sottende un arco pari al raggio; poiché la circonferenza ha lunghezza c = 2πr, in essa sono contenuti 2π raggi; di conseguenza un angolo giro di 360° corrisponderà a 2π radianti.

Ciò premesso, l’angolo piano α è definito dal rapporto  α = l / r tra la lunghezza  l dell’arco di circonferenza sotteso ed il raggio r della circonferenza.

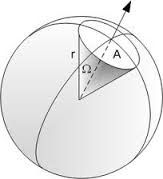
Per quanto riguarda l’angolo solido Ω si fa riferimento ad una sfera e lo si definisce come il rapporto Ω = A / r2 tra l’area A della calotta intercettata sulla sfera ed il quadrato del raggio r della sfera.

L’unità di misura dell’angolo solido è lo steradiante ( sr ), che corrisponde all’angolo che intercetta una calotta sferica avente un’area pari al quadrato del raggio; poiché la superficie della sfera misura  4πr2 , l’angolo solido totale misura 4π steradianti.

Il FLUSSO LUMINOSO ( Φ )

Una sorgente luminosa S di intensità I posta sul vertice di un angolo solido Ω  invia all’interno di esso un flusso luminoso Φ = I x Ω.

L’unità di misura del flusso luminoso è il lumen ( lm ) che corrisponde al flusso inviato dalla intensità di 1 candela in un angolo solido di uno steradiante : 1 lumen = 1 candela x 1 steradiante.

L’ILLUMINAMENTO di una superficie  ( E )

L’illuminamento di una superficie è determinato dal rapporto E = Φ / A tra il flusso luminoso che investe perpendicolarmente la superficie e l’area della superficie stessa. L’unità di misura dell’illuminamento è il lux: 1 lux = 1 lumen / 1 m2.

Da queste definizioni è possibile dedurre la relazione E = I / r2 , nota come Legge di Lambert, secondo la quale l’illuminamento varia secondo il quadrato della distanza.

La LUMINANZA di una sorgente ( L )

La luminanza  è definita come il rapporto L = I / A  tra l’intensità luminosa emessa da una sorgente verso una superficie normale alla direzione del flusso e l’area della superficie stessa. La sua unità di misura è il nit: 1 nit = 1 cd / 1 m^2.

La grandezza è indicativa dell’abbagliamento che può indurre una sorgente. Un tubo fluorescente è meno abbagliante di una lampada ad incandescenza (in cui l’intensità è concentrata sul filamento).

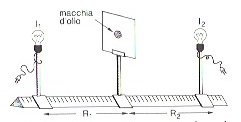
Una macchia per fotometro

Una macchia di unto su in foglio di carta appare normalmente scura, ma se la si osserva controluce diventa chiara (traslucida). Bastano alcune prove per capire che quando prevale l’illuminamento anteriore la macchia appare scura, quando prevale quello posteriore la macchia appare chiara. Quando, invece, le due facce del foglio sono illuminate allo stesso modo, la macchia sembra scomparire.

Sulla base di questa osservazione è possibile costruire un semplice fotometro, che permette di confrontare l’intensità di una sorgente con quella di una sorgente campione ( ad es. una candela ).

Per la legge di Lambert sarà: I1/ I2 = ( R1 ) 2 / (R2 )2