Tra i testimoni che possiamo interrogare per cercare altre prove a favore della ipotesi di una propagazione rettilinea della luce, le ombre sono certamente tra quelli più importanti.

Sono testimoni attendibili? Le ombre, a cominciare da Platone, non godono di grande reputazione.

Le ombre sono sempre state circondate dal sospetto e dalla paura.

Sono piatte e sfuggenti, senza alcuna consistenza. Nell’ombra si trama e si tendono agguati. C’è l’ombra del dubbio e l’ombra della minaccia.  Una persona in gravi difficoltà si riduce “all’ombra di se stessa”.  Una persona irascibile ha un carattere ombroso. E così via denigrando.

 Roberto Casati nel suo splendido libro La scoperta dell’ombra riabilita completamente l’ombra e ne fa un testimone molto attendibile delle relazioni che essa intrattiene con gli oggetti e le sorgenti di luce.

L’OMBRA PUO’ ESSERE UNA PROVA DELLA PROPAGAZIONE DELLA LUCE?

Abbiamo visto come l’idea che la luce si propaghi non sia del tutto scontata. Esiste anche una visione statica per la quale la luce è una sorta di “stato di visibilità”, che si stabilisce istantaneamente in tutto lo spazio, non appena viene accesa la sorgente.

A ben guardare, il fatto che dietro l’oggetto si formi una zona d’ombra, sembra deporre a favore dell’ipotesi di una propagazione della luce: i raggi che colpiscono l’oggetto, ne illuminano la parte anteriore, ma non riescono a raggiungere né quella posteriore né lo schermo . Se bastasse la semplice accensione della sorgente per restituire a tutto lo spazio la sua trasparenza ( come previsto dal modello statico), non si capirebbe perché proprio la porzione di spazio racchiusa nel “cono d’ombra” (tra l’oggetto e l’ombra)  dovrebbe rimanere esclusa da questo effetto.

PUO’ DIMOSTRARE CHE LA PROPAGAZIONE SIA ANCHE RETTILINEA?

Che bisogno c’è, potremmo chiederci, di cercare delle prove per una ipotesi che ci appare così naturale e intuitiva, come quella della propagazione della luce per raggi rettilinei?

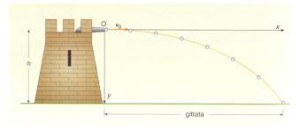
Per la verità, ce ne sarebbe almeno un’altra di ipotesi alternativa, ancor più naturale e familiare, ed è quella che ci viene suggerita dall’esperienza quotidiana degli oggetti che vengono lanciati o, purtroppo, di proiettili che vengono sparati. Questa esperienza ci dice che a causa della gravità l’oggetto descrive una traiettoria parabolica, ed anche quando viene lanciato con una grande velocità orizzontale (come nel caso dei proiettili), la traiettoria mantiene una forma parabolica, sebbene molto più “allungata”.

Chi ci impedisce di pensare che anche la luce possa risentire della gravità e descrivere (sulla lunga distanza) una traiettoria curva?

Per verificarlo dovremmo uscire dalle piccole dimensioni del nostro laboratorio e guardare la luce delle stelle che arriva da noi dopo aver percorso enormi distanze. Ma questo, per il momento, è un compito che lasciamo agli astronomi, limitando le nostre osservazioni alla  scala molto più ridotta della nostra aula. Non dovremo mai dimenticare, però, che le conclusioni alle quali arriveremo avranno validità solo nell’ambito limitato nel quale le abbiamo verificate.

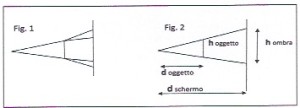
Come se questo non bastasse a complicarci le cose, ci sono almeno altre due ipotesi del tutto ragionevoli sulle traiettorie che i raggi luminosi potrebbero seguire. Non possiamo escludere, infatti, che sfiorando l’oggetto i raggi possano subire delle attrazioni o delle repulsioni da parte di esso (fig 1).

In entrambi i casi l’ombra avrebbe dimensioni diverse da quelle ipotizzate per la propagazione rettilinea ( fig. 2).

Dopo questo chiarimento preliminare potremo passare ad osservare e registrare le variazioni che si producono nelle dimensioni dell’ombra in seguito allo spostamento della sorgente, dell’oggetto e dello schermo.

Si comincerà, così, ad intuire che esse dipendono da quanto l’oggetto e lo schermo distano dalla sorgente.

Indicate con hi , ho , di  e do  le   dimensioni dell’ombra e dell’oggetto, e le rispettive distanze dalla sorgente, si noterà che solo nel caso di una propagazione rettilinea si verificherà la relazione di proporzionalità :

hi  /  ho  =  di  /  do

Poiché i dati raccolti confermano con buona approssimazione l’esistenza di questa relazione, possiamo cominciare a considerare la propagazione rettilinea della luce come una vera e propria legge fisica.

 Pagina successiva >>